Unlocking Success: Mastering Algebra 1 Big Ideas Math – Section 7.6 #3 Explained!
Big Ideas Math Section 7.6 #3 How to factor a trinomial with the AC Grouping Method ROHS DIstance Learning Algebra 1.
source
Understanding Algebra 1 Big Ideas Math: Section 7.6 #3
In Algebra 1, Section 7.6 focuses on the key concepts of systems of equations and how to solve them using various methods. Problem #3 often serves as an excellent illustration of these principles. In this article, we’ll break down the important ideas covered in this section and provide strategies for solving problems like #3 effectively.
Key Concepts
Systems of Equations: A system of equations consists of two or more equations with the same set of variables. The solution to the system is the point where the equations intersect on a graph, representing values that satisfy all equations simultaneously.
- Methods of Solving:
- Graphing: You can plot each equation on the same set of axes and identify where they intersect.
- Substitution: Solve one of the equations for one variable and then substitute that expression into the other equation.
- Elimination: Add or subtract the equations to eliminate one variable, making it easier to solve for the other variable.
Breaking Down Problem #3
While the specific content of problem #3 can vary, let’s assume it involves solving a simple system of linear equations. Here’s how to approach it systematically:
Identify the Equations: Start by clearly writing down the equations provided in the problem. Ensure they are in standard form, which typically looks like (Ax + By = C).
Choose a Method: Decide which method seems most straightforward for the equations. For many students, the substitution method is often the simplest when one of the equations is easily solvable for one variable.
Solve the System:
Using Substitution: If one equation is already solved for one variable:
- Substitute this expression into the other equation.
- Simplify and solve for the other variable.
- Once you have one variable, substitute back to find the second variable.
- Using Elimination: If neither equation is easily solvable, consider aligning the equations for elimination:
- Multiply equations if necessary to line up coefficients for one variable.
- Add or subtract equations to eliminate that variable.
- Solve for the remaining variable and backtrack to find the other.
Check Your Solution: Once you’ve found your solution, plug the values back into the original equations to verify that they satisfy both equations.
- Graphical Representation: Optionally, graphing the equations can provide a visual check. The point where the lines intersect is your solution.
Conclusion
Understanding how to work through a system of equations in problems like Algebra 1 Big Ideas Math Section 7.6 #3 is crucial. Mastery of techniques such as substitution and elimination not only prepares students for standardized tests and further math courses but also enhances logical thinking skills. Practice is key; as you work through various problems, you’ll become more familiar with the concepts and techniques necessary to solve systems of equations efficiently.
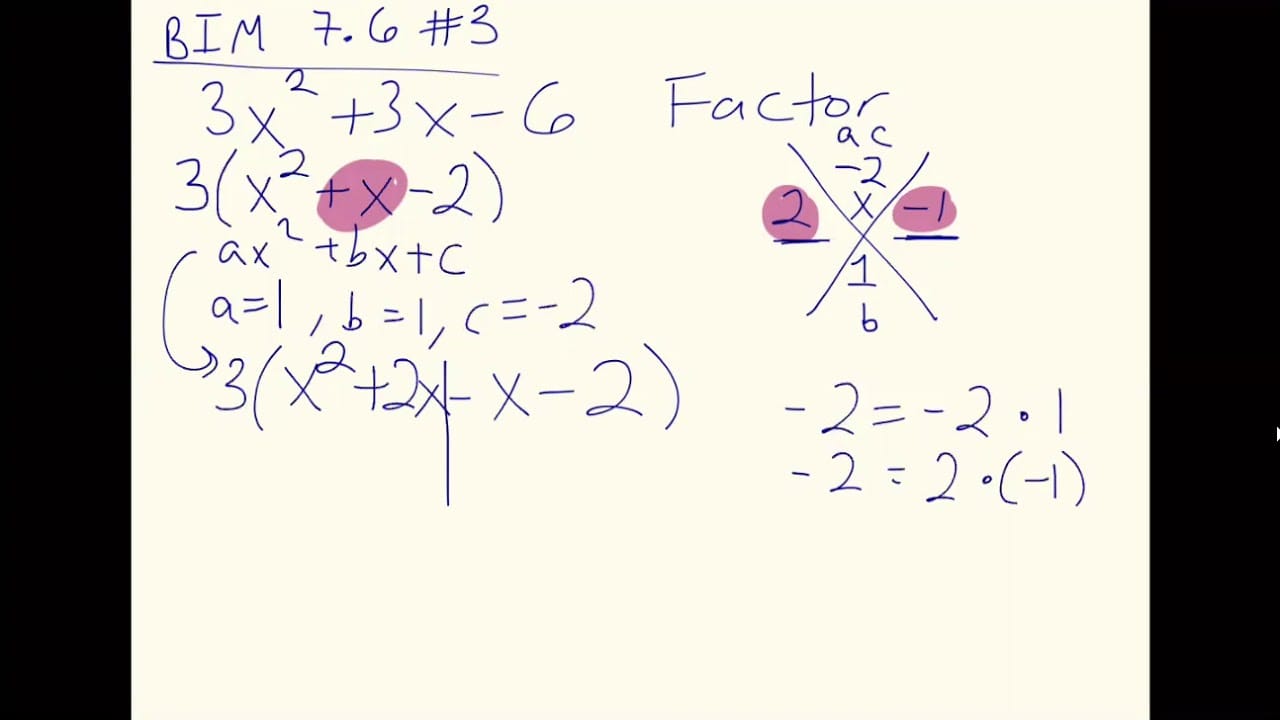














Post Comment